# Hack Your Skills! to be Professional Mechatronics
Pada step pertama, hitung jalur asal dengan jalur yang mungkin untuk dilewati. Jalur yang mungkin hanya Bandung (270km) dan Cirebon (327km). Urutkan jarak tersebut berdasarkan yang terpendek. jarak yang terpendek akan dipilih untuk menghitung jarak selanjutnya, sedangkan jarak terpendek kedua akan dijadikan treshold atau patokan untuk dihitung apabila hasil dari jalur yang dibuka dari jarak terpendek lebih besar daripada jarak jalur kedua tersebut. Pada step awal, jarak minimal adalah Jakarta-Bandung, dan yang menjadi treshold adalah jarak Jakarta-Cirebon.
Step kedua yang dibuka adalah jalur Jakarta-Bandung. Kemungkinan yang bisa dilewati adalah jalur Jakarta-Bandung-Cirebon (390km) dan Jakarta-Bandung-Yogyakarta (643). Selanjutnya jarak-jarak tersebut dibandingkan dan dipilih jalur terpendek. Jalur yang terpendek adalah Jakarta-Cirebon dan jalur terpendek kedua adalah Jakarta-Bandung-Cirebon. Sehingga jalur yang akan dibuka selanjutnya adalah jalur Jakarta-Cirebon dan yang menjadi treshold adalah jalur Jakarta-Bandung-Cirebon. Begitu seterusnya hingga didapatkan jarak terpendek untuk menghubungkan semua kota.
Dalam proses pencarian, peta tersebut ‘dibaca’ dengan fungsi possible() untuk mengetahui kemungkinan jalur yang akan dilalui dari suatu kota. Fungsi possible() tampak pada Source Code Fungsi possible() , inputnya adalah id kota, dan ouputnya adalah daftar kota yang mungkin dilalui. Pada kode tersebut dilalukan perulangan pada peta dan mencari jalur yang mungkin untuk kota dengan id yang cocok.
PHP : Penyelesaian Traveling Salesman Problem (TSP) Menggunakan Algoritma Recursive Best First Search (RBFS)
Bahasan: Tulisan ini adalah salah satu tugas Kecerdasan Komputasional. ABSTRAK Travelling Salesman Problem (TSP) merupakan sebuah permasala...
Published at Sabtu, 18 Juli 2015, Updated at Sabtu, 18 Juli 2015
Reviewed by dr. on
Rating: 4.7
PHP : Penyelesaian Traveling Salesman Problem (TSP) Menggunakan Algoritma Recursive Best First Search (RBFS)
Tulisan ini adalah salah satu tugas Kecerdasan Komputasional.
ABSTRAK
Travelling Salesman Problem (TSP) merupakan sebuah permasalahan optimasi yang dapat diterapkan pada berbagai kegiatan seperti routing. Masalah optimasi TSP terkenal dan telah menjadi standar untuk mencoba algoritma yang komputational. Pokok permasalahan dari TSP adalah seorang salesman harus mengunjungi sejumlah kota yang diketahui jaraknya satu dengan yang lainnya. Semua kota yang ada harus dikunjungi oleh salesman tersebut dan kota tersebut hanya boleh dikunjungi tepat satu kali. Permasalahannya adalah bagaimana salesman tersebut dapat mengatur rute perjalanannya sehingga jarak yang ditempuhnya merupakan rute yang optimum yaitu jarak minimum terbaik. Dalam makalah ini penyelesaian kasus TSP diselesaikan dengan algoritma Recursive Best First Search (RBFS).
A. LATAR BELAKANG MASALAH
Travelling Salesman Problem (TSP) merupakan permasalahan pedagang keliling dalam mencari lintasan terpendek dari semua kota yang dikunjunginya. Dengan syarat kota tersebut hanya boleh dikunjungi satu kali. Banyak permasalahan yang dapat direpresentasikan dalam bentuk Travelling Salesman Problem. Persoalan ini sendiri menggunakan representasi graf untuk memodelkan persolan yang diwakili sehingga lebih memudahkan penyelesaiannya. Diantaranya permasalahan yang dapat direpresentasikan dengan TSP ialah masalah transportasi, efisiensi pengiriman surat atau barang, perancangan pemasangan pipa saluran, proses pembuatan PCB (Printed Circuit Board) dan lain–lain.
Ada beberapa algoritma dan metode yang bisa menyelesaikan TSP ini, antara lain: algoritma Brute Force dengan complete Enumeration, algoritma Branch and Bound, Greedy Heuristik. Dalam Algoritma Bruto Force, hal yang dilakukan ialah dengan cara mengenumerasi seluruh kemungkinan rute yang akan ditempuh. Setelah itu, akan dibandingkan dari seluruh kemungkinan rute yang telah dienumerasi tersebut, rute mana yang memiliki lintasan/bobot yang paling minimum. Namun, jumlah enumerasi dari algoritma ini ialah (n-1)! Yang akan memerlukan waktu yang sangat lama untuk mendapatkan panjang lintasan paling minimum jika n bernilai sangat besar. Seperti Algoritma Brute Force yang mengenumerasi satu per satu kemungkinan jalur yang akan ditempuh, Algoritma Branch and bound ternyata tidak memiliki kompleksitas waktu yang lebih baik dimana algoritma ini juga memilki kompleksitas waktu (n-1)! Dan sangat membutuhkan waktu yang sangat lama untuk mendapatkan panjang lintasan paling minimum jika n bernilai sangat besar.
Sedangkan pada greedy heuristik, pemilihan lintasan akan dimulai pada lintasan yang memilki nilai paling minimum, algoritma ini akan memilih kota selanjutnya yang belum dikunjungi yang mempunyai bobot paling minimum/kota terdekat sampai swmua kota tersebut dikunjungi dan kemudian kembali ke kota awal, tetapi hasil yang didapat bisa sangat jauh dari hasil optimal, semakin banyak kota yang dikunjungi semakin besar pula perbedaan yang dicapai.
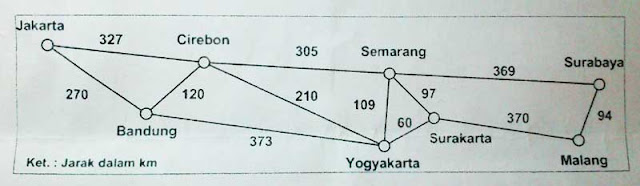
Algoritma Heuristik merupakan salah satu algoritma alternatif yang dapat digunakan sebab prosesnya cepat dan memberikan hasil yang diinginkan. Algoritma Heuristik adalah algoritma yang mencari solusi terbaik untuk kasus yang merupakan bagian atau irisan dari permasalahan total dengan harapan dapat menghasilkan solusi optimal untuk keseluruhan kasus melalui proses tambahan, yaitu mencari bobot minimum dengan menggunakan Recursive Best First Search (RBFS) sehingga menghasilkan routing dari graf yang memiliki nilai optimal. Permasalahan pada makalah ini bisa dilihat pada Gambar 1, yaitu mencari jarak terpendek terbaik yang bisa ditempuh oleh sales dan setiap kota hanya boleh dikunjungi satu kali.
 |
| Gambar 1. Peta jalur antar kota yang harus dilewati oleh sales |
B. RECURSIVE BEST-FIRST SEARCH (RBFS)
Recursive Best-First Search merupakan algoritma pencarian terbimbing yang mirip dengan algoritma standar Best First Search yang bersifat linear. Desain algoritmanya juga mirip dengan Depth-First Search walaupun dengan model yang sangat berbeda.
Cara kerja RBFS yaitu tetap memperhatikan jalur teratas, kalau misalkan pada tree, maka tree paling atas. Apabila ada jalur yang tidak sesuai, maka jalur teratas akan langsung mengubahnya. Pada saat operasi, setiap operasi yang akan dipilih adalah jalur yang terpendek, dan setiap ada jalur baru, maka jalur teratas akan diurutkan berdasarkan nilai cost yang terkecil.
Hal tersebut akan dilakukan hingga titik akhir adalah jalur yang dituju dan cost yang ditemukan pada jalur terakhir ini lebih kecil dari jalur-jalur yang sudah dilewati sebelumnya. Berikut ini adalah presudocode algoritma untuk RBFS.
C. PEMODELAN
Gambar 2. merupakan representasi bentuk pohon dari peta jalur antar kota yang akan dicari solusinya. Garis putus-putus menunjukkan bahwa jalur yang bisa menjadi solusi adalah jalur yang melewati seluruh kota dan tepat satu kali untuk masing-masing kota. Sedangkan jarak antar kota berdasarkan jalur yang ada pata peta dapat dilihat pada tabel 1.
 |
| Gambar 2. Representasi jalur antar kota dalam kasus TSP |
Tabel 1. Tabel jarak antar kota (dalam km)
Berdasarkan pohon pada Gambar 2, maka proses pencarian RBFS akan dilakukan dengan cara membandingkan setiap simpul yang dilewati dan dicari simpul yang memiliki cost atau jarak yang paling kecil sesuai dengan algoritma pada RBFS. Proses perhitungan untuk menemukan jalur terpendek dengan metode RBFS akan dijelaskan secara singkat seperti pada Tabel 2.
Pada step pertama, hitung jalur asal dengan jalur yang mungkin untuk dilewati. Jalur yang mungkin hanya Bandung (270km) dan Cirebon (327km). Urutkan jarak tersebut berdasarkan yang terpendek. jarak yang terpendek akan dipilih untuk menghitung jarak selanjutnya, sedangkan jarak terpendek kedua akan dijadikan treshold atau patokan untuk dihitung apabila hasil dari jalur yang dibuka dari jarak terpendek lebih besar daripada jarak jalur kedua tersebut. Pada step awal, jarak minimal adalah Jakarta-Bandung, dan yang menjadi treshold adalah jarak Jakarta-Cirebon.
Step kedua yang dibuka adalah jalur Jakarta-Bandung. Kemungkinan yang bisa dilewati adalah jalur Jakarta-Bandung-Cirebon (390km) dan Jakarta-Bandung-Yogyakarta (643). Selanjutnya jarak-jarak tersebut dibandingkan dan dipilih jalur terpendek. Jalur yang terpendek adalah Jakarta-Cirebon dan jalur terpendek kedua adalah Jakarta-Bandung-Cirebon. Sehingga jalur yang akan dibuka selanjutnya adalah jalur Jakarta-Cirebon dan yang menjadi treshold adalah jalur Jakarta-Bandung-Cirebon. Begitu seterusnya hingga didapatkan jarak terpendek untuk menghubungkan semua kota.
Tabel 2. Step-step pencarian algoritma RBFS
D. IMPLEMENTASI METODE
Model komputasi algoritma untuk menyelesaikan kasus TSP dengan RBFS yaitu dibuat dengan bahasa pemrograman PHP . Hal yang pertama dilakukan adalah pemetaan kota dan jarak antar kota. Peta dibuat dalam bentuk array objek dimana untuk masing-masing kota berisi ID kota, Nama kota, jalur yang mungkin dilalui sekaligus jarak antara kota denga jalur tersebut. Pada source code representasi peta dalam bahsa pemrograman menunjukkan kota Jakarta dan kota Bandung. Kota jakarta memiliki id ‘jkt’ dan jalur yang mungkin dilalui adalah Jakarta-Bandung (bdg) dengan jarak 270 km dan Jakarta-Cirebon (crb) dengan jarak 327 km. Sedangkan kota Bandung, jalur yang mungkin dilewati adalah Bandung-Cirebon (crb) dengan jarak 120 km dan Bandung-Yogyakarta (ygy) dengan jarak 373 km.
Representasi peta dalam bahasa pemrograman
$peta = array(
'jkt' => (object)array(
'id' => 'jkt',
'name' => 'Jakarta',
'path' => array(
'bdg' => 270,
'crb' => 327
)
),
'bdg' => (object)array(
'id' => 'bdg',
'name' => 'Bandung',
'path' => array(
'crb' => 120,
'ygy' => 373
)
),
'crb' => (object)array(
'id' => 'crb',
'name' => 'Cirebon',
'path' => array(
'smg' => 305,
'ygy' => 210
)
),
'smg' => (object)array(
'id' => 'smg',
'name' => 'Semarang',
'path' => array(
'ygy' => 109,
'srkt' => 97,
'sby' => 365
)
),
'ygy' => (object)array(
'id' => 'ygy',
'name' => 'Yogyakarta',
'path' => array(
'srkt' => 60
)
),
'srkt' => (object)array(
'id' => 'srkt',
'name' => 'Surakarta',
'path' => array(
'mlg' => 370
)
),
'sby' => (object)array(
'id' => 'sby',
'name' => 'Surabaya',
'path' => array(
'mlg' => 94
)
),
'mlg' => (object)array(
'id' => 'mlg',
'name' => 'Malang',
'path' => array()
)
);
Dalam proses pencarian, peta tersebut ‘dibaca’ dengan fungsi possible() untuk mengetahui kemungkinan jalur yang akan dilalui dari suatu kota. Fungsi possible() tampak pada Source Code Fungsi possible() , inputnya adalah id kota, dan ouputnya adalah daftar kota yang mungkin dilalui. Pada kode tersebut dilalukan perulangan pada peta dan mencari jalur yang mungkin untuk kota dengan id yang cocok.
Source Code Fungsi possible()
function possible($kota){
$ret = array();
foreach($this->peta as $next){
foreach($next->path as $key=>$target){
$tmp = array();
if($next->id == $kota){
$tmp['id'] = $key;
$tmp['len'] = $target;
array_push($ret,$tmp);
}else{
if($key == $kota){
$tmp['id'] = $next->id;
$tmp['len'] = $next->path[$kota];
array_push($ret,$tmp);
}
}
}
}
return $ret;
}
Fungsi utama untuk RBFS ada pada fungsi route(). Fungsi route() membutuhkan input kota yang sedang dibuka (di-expand / open) dan menghasilkan jalur dengan cost yang minimal dan jalur yang akan dijadikan backup / treshold. Source code Potongan fungsi route() untuk menghitung path merupakan potongan source code untuk fungsi route(). Pertama akan dicari jalur yang mungkin dilewati dengan pemanggilan fungsi possible(). Setelah itu daftar jalur yang akan dilewati akan dihitung satu-persatu dengan perulangan. Masing-masing jalur akan dihitung besar cost dari jalur awal yaitu pada variabel $tmp[lenmin].
Potongan fungsi route() untuk menghitung path
function route($start){
$next = $this->possible($start['id']);
$lastone = true;
foreach($next as $nxt){
$chkpath = $start['path'].'-'.$nxt['id'];
$chkp = explode('-',$chkpath);
if(!strpos('x'.$start['path'],$nxt['id']) || ($chkp[0]==$nxt['id'] && sizeof($chkp)==sizeof($this->peta)+1)){
$tmp = $nxt;
if($start['path']==''){
$tmp['lenmin'] = $nxt['len'];
$tmp['path'] = $start['id'].'-'.$tmp['id'];
}else{
$tmp['lenmin'] = $start['lenmin'] + $nxt['len'];
$tmp['path'] = $start['path'].'-'.$tmp['id'];
}
array_push($this->routing, $tmp);
$lastone = false;
}
}
usort($this->routing,function($a,$b){ return $a['lenmin'] - $b['lenmin']; });
$open = $this->routing[0];
$back = $this->routing[1];
if($open['path']){
$tmp = array();
$tmp['path'] = $this->KOTA($open['path']);
$tmp['cost'] = $open['lenmin'];
array_push($this->result, $tmp);
}
if($open['path']!=''){
unset($this->routing[0]);
$this->route($open);
}
}
Setelah masing-masing cost dihitung, maka semua kemungkinan jalur yang ada akan diurutkan berdasarkan cost yang terkecil dengan fungsi usort(). Seletah diurutkan, makan jalur dengan cost terkecil akan dibuka (variabel $open) dan jalur terkecil kedua akan dijadikan treshold untuk perbandingan (variabel $back). Selanjutnya pembukaan jalur baru dilakukan pada bagian $this->route($open).
Gambar 7. adalah hasil eksekusi program ketika dijalankan. Jika memilih jalur awal adalah Jakarta, maka sistem membutuhkan 107 kali perulangan dengan jalur terbaik Jakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta-Yogyakarta-Bandung-Jakarta dengan jarak yang ditempuh 2164 km atau sebaliknya. Step-step pencarian jalur yang lengkap bisa dilihat pada tabel 3.
 |
| Gambar 7. Hasil eksekusi program |
Tabel 3. Step-step pencarian jalur terpendek dengan kota awal Jakarta
Step Rute Cost 1 Jakarta-Bandung 270 2 Jakarta-Cirebon 327 3 Jakarta-Bandung-Cirebon 390 4 Jakarta-Cirebon-Bandung 447 5 Jakarta-Cirebon-Yogyakarta 537 6 Jakarta-Cirebon-Yogyakarta-Surakarta 597 7 Jakarta-Bandung-Cirebon-Yogyakarta 600 8 Jakarta-Cirebon-Semarang 632 9 Jakarta-Bandung-Yogyakarta 643 10 Jakarta-Cirebon-Yogyakarta-Semarang 646 11 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta 660 12 Jakarta-Cirebon-Yogyakarta-Surakarta-Semarang 694 13 Jakarta-Bandung-Cirebon-Semarang 695 14 Jakarta-Bandung-Yogyakarta-Surakarta 703 15 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang 709 16 Jakarta-Cirebon-Semarang-Surakarta 729 17 Jakarta-Cirebon-Semarang-Yogyakarta 741 18 Jakarta-Cirebon-Yogyakarta-Semarang-Surakarta 743 19 Jakarta-Bandung-Yogyakarta-Semarang 752 20 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Semarang 757 21 Jakarta-Cirebon-Semarang-Surakarta-Yogyakarta 789 22 Jakarta-Bandung-Cirebon-Semarang-Surakarta 792 23 Jakarta-Bandung-Yogyakarta-Surakarta-Semarang 800 24 Jakarta-Cirebon-Semarang-Yogyakarta-Surakarta 801 25 Jakarta-Bandung-Cirebon-Semarang-Yogyakarta 804 26 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surakarta 806 27 Jakarta-Cirebon-Bandung-Yogyakarta 820 28 Jakarta-Bandung-Yogyakarta-Semarang-Surakarta 849 29 Jakarta-Bandung-Cirebon-Semarang-Surakarta-Yogyakarta 852 30 Jakarta-Bandung-Yogyakarta-Cirebon 853 31 Jakarta-Bandung-Cirebon-Semarang-Yogyakarta-Surakarta 864 32 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta 880 33 Jakarta-Cirebon-Yogyakarta-Bandung 910 34 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang 929 35 Jakarta-Cirebon-Yogyakarta-Surakarta-Malang 967 36 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Semarang 977 37 Jakarta-Cirebon-Semarang-Surabaya 997 38 Jakarta-Cirebon-Yogyakarta-Semarang-Surabaya 1011 39 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surakarta 1026 40 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Malang 1030 41 Jakarta-Bandung-Yogyakarta-Semarang-Cirebon 1057 42 Jakarta-Cirebon-Yogyakarta-Surakarta-Semarang-Surabaya 1059 43 Jakarta-Bandung-Cirebon-Semarang-Surabaya 1060 44 Jakarta-Cirebon-Yogyakarta-Surakarta-Malang-Surabaya 1061 45 Jakarta-Bandung-Yogyakarta-Surakarta-Malang 1073 46 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surabaya 1074 47 Jakarta-Cirebon-Semarang-Surabaya-Malang 1091 48 Jakarta-Cirebon-Semarang-Surakarta-Malang 1099 49 Jakarta-Cirebon-Yogyakarta-Semarang-Surabaya-Malang 1105 50 Jakarta-Bandung-Yogyakarta-Surakarta-Semarang-Cirebon 1105 51 Jakarta-Cirebon-Yogyakarta-Semarang-Surakarta-Malang 1113 52 Jakarta-Cirebon-Semarang-Yogyakarta-Bandung 1114 53 Jakarta-Bandung-Yogyakarta-Semarang-Surabaya 1117 54 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Semarang-Surabaya 1122 55 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Malang-Surabaya 1124 56 Jakarta-Cirebon-Yogyakarta-Surakarta-Semarang-Surabaya-Malang 1153 57 Jakarta-Bandung-Cirebon-Semarang-Surabaya-Malang 1154 58 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang 1158 59 Jakarta-Cirebon-Semarang-Surakarta-Yogyakarta-Bandung 1162 60 Jakarta-Bandung-Cirebon-Semarang-Surakarta-Malang 1162 61 Jakarta-Bandung-Yogyakarta-Surakarta-Semarang-Surabaya 1165 62 Jakarta-Bandung-Yogyakarta-Surakarta-Malang-Surabaya 1167 63 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surabaya-Malang 1168 64 Jakarta-Cirebon-Semarang-Yogyakarta-Surakarta-Malang 1171 65 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surakarta-Malang 1176 66 Jakarta-Cirebon-Semarang-Surakarta-Malang-Surabaya 1193 67 Jakarta-Cirebon-Yogyakarta-Semarang-Surakarta-Malang-Surabaya 1207 68 Jakarta-Bandung-Yogyakarta-Semarang-Surabaya-Malang 1211 69 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Semarang-Surabaya-Malang 1216 70 Jakarta-Bandung-Yogyakarta-Semarang-Surakarta-Malang 1219 71 Jakarta-Bandung-Cirebon-Semarang-Yogyakarta-Surakarta-Malang 1234 72 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Malang 1250 73 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surakarta 1255 74 Jakarta-Bandung-Cirebon-Semarang-Surakarta-Malang-Surabaya 1256 75 Jakarta-Bandung-Yogyakarta-Surakarta-Semarang-Surabaya-Malang 1259 76 Jakarta-Cirebon-Semarang-Yogyakarta-Surakarta-Malang-Surabaya 1265 77 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surakarta-Malang-Surabaya 1270 78 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surabaya 1294 79 Jakarta-Bandung-Yogyakarta-Semarang-Surakarta-Malang-Surabaya 1313 80 Jakarta-Bandung-Cirebon-Semarang-Yogyakarta-Surakarta-Malang-Surabaya 1328 81 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Semarang-Surabaya 1342 82 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Malang-Surabaya 1344 83 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surabaya-Malang 1388 84 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surakarta-Malang 1396 85 Jakarta-Cirebon-Yogyakarta-Surakarta-Malang-Surabaya-Semarang 1426 86 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Semarang-Surabaya-Malang 1436 87 Jakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta 1461 88 Jakarta-Cirebon-Yogyakarta-Semarang-Surabaya-Malang-Surakarta 1475 89 Jakarta-Bandung-Cirebon-Yogyakarta-Surakarta-Malang-Surabaya-Semarang 1489 90 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surakarta-Malang-Surabaya 1490 91 Jakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta-Yogyakarta 1521 92 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surabaya 1523 93 Jakarta-Bandung-Cirebon-Semarang-Surabaya-Malang-Surakarta 1524 94 Jakarta-Bandung-Yogyakarta-Surakarta-Malang-Surabaya-Semarang 1532 95 Jakarta-Bandung-Cirebon-Yogyakarta-Semarang-Surabaya-Malang-Surakarta 1538 96 Jakarta-Bandung-Yogyakarta-Semarang-Surabaya-Malang-Surakarta 1581 97 Jakarta-Bandung-Cirebon-Semarang-Surabaya-Malang-Surakarta-Yogyakarta 1584 98 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surabaya-Malang 1617 99 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surakarta-Malang 1625 100 Jakarta-Cirebon-Bandung-Yogyakarta-Surakarta-Malang-Surabaya-Semarang 1709 101 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surakarta-Malang-Surabaya 1719 102 Jakarta-Cirebon-Bandung-Yogyakarta-Semarang-Surabaya-Malang-Surakarta 1758 103 Jakarta-Bandung-Yogyakarta-Surakarta-Malang-Surabaya-Semarang-Cirebon 1837 104 Jakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta-Yogyakarta-Bandung 1894 105 Jakarta-Bandung-Yogyakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta 1987 106 Jakarta-Bandung-Yogyakarta-Surakarta-Malang-Surabaya-Semarang-Cirebon-Jakarta 2164 107 Jakarta-Cirebon-Semarang-Surabaya-Malang-Surakarta-Yogyakarta-Bandung-Jakarta 2164
E. KESIMPULAN
Penggunaan RBFS dalam mencari rute terpendek terbaik untuk kasus ini dengan kota asala Jakarta adalah jalur :
Jakarta – Cirebon – Semarang – Surabaya – Malang – Surakarta – Yogyakarta – Bandung - Jakarta
atau jalur sebaliknya dengan pangjang rute adalah 2164 km. Sampel aplikasi bisa diakses di alamat http://lab.elangsakti.com/tsp/ .
F. REFERENSI
Pearl, J. Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley, 1984. p. 48.
Russell, S. J., Norvig, P, Artificial Intelligence: A Modern Approach, 2003.
Source Code lengkap Class RBFS:
<?php
class TSP{
var $peta = array();
var $routing = array();
var $result = array();
function start( $kota ){
$start = array('id'=>$kota, 'path'=>'');
$this->route($start);
return $this->result;
}
function setPeta($peta){
$this->peta = $peta;
}
function possible($kota){
$ret = array();
foreach($this->peta as $next){
foreach($next->path as $key=>$target){
$tmp = array();
if($next->id == $kota){
$tmp['id'] = $key;
$tmp['len'] = $target;
array_push($ret,$tmp);
}else{
if($key == $kota){
$tmp['id'] = $next->id;
$tmp['len'] = $next->path[$kota];
array_push($ret,$tmp);
}
}
}
}
return $ret;
}
function route($start){
$next = $this->possible($start['id']);
$lastone = true;
foreach($next as $nxt){
$chkpath = $start['path'].'-'.$nxt['id'];
$chkp = explode('-',$chkpath);
if(!strpos('x'.$start['path'],$nxt['id']) || ($chkp[0]==$nxt['id'] && sizeof($chkp)==sizeof($this->peta)+1)){
$tmp = $nxt;
if($start['path']==''){
$tmp['lenmin'] = $nxt['len'];
$tmp['path'] = $start['id'].'-'.$tmp['id'];
}else{
$tmp['lenmin'] = $start['lenmin'] + $nxt['len'];
$tmp['path'] = $start['path'].'-'.$tmp['id'];
}
array_push($this->routing, $tmp);
$lastone = false;
}
}
usort($this->routing,function($a,$b){ return $a['lenmin'] - $b['lenmin']; });
$open = $this->routing[0];
$back = $this->routing[1];
if($open['path']){
$tmp = array();
$tmp['path'] = $this->KOTA($open['path']);
$tmp['cost'] = $open['lenmin'];
array_push($this->result, $tmp);
}
if($open['path']!=''){
unset($this->routing[0]);
$this->route($open);
}
}
function KOTA( $path ){
foreach($this->peta as $kota){
$path = str_replace($kota->id,$kota->name,$path);
}
return $path;
}
}
?>
Top Artikel :
PHP : Penyelesaian Traveling Salesman Problem (TSP) Menggunakan Algoritma Recursive Best First Search (RBFS)
Bahasan: Tulisan ini adalah salah satu tugas Kecerdasan Komputasional. ABSTRAK Travelling Salesman Problem (TSP) merupakan sebuah permasala...
Published at Sabtu, 18 Juli 2015, Updated at Sabtu, 18 Juli 2015
Reviewed by dr. on
Rating: 4.7
Langganan:
Posting Komentar
(
Atom
)
cara makeknya gimana yak ko0k nge blank
BalasHapusSebenarnya kalo dari petanya sudah terbaca hasilya pak. Tidak perlu pakai program. Jika kita pakai lintasan yang menyebrang pasti akan lebih besar jaraknya. Jika ditempuh dengan lintasan lurus dan putar arah akan lebih efektif. Tapi saya sangat senang dengan artikel ini. Sangat diperlukan memang untuk pembuktian secara angka yang jelas dan menyeluruh. Apalagi buat lembaga or perusahaan. Pasti ingin tahu kebenarannya. Semangat terus pak untuk berkarya. Saya sangat suka tulisan/artikel nya pak. Terima kasih banyak
BalasHapusTerima kasih sudah mampir pak Agus. :)
HapusSecara visual, di peta memang sudah terbaca hasilnya. Tujuan pembuatan program komputer adalah supaya peta tersebut juga bisa dibaca oleh komputer, sehingga otomatisasi pembacaan jarak di peta tidak perlu dihitung manual oleh manusia. Seperti itulah salah satu manfaat dari sistem cerdas dg komputer. Salam.
Terima kasih Pak Hari Santoso tulisan bagusnya ini. Terstruktur dan lengkap sampai implementasi programnya di PHP. Saya suka hehe.
BalasHapus